Двух- и трехмерная визуализация волны возбуждения миокарда с помощью компьютерного моделирования с использованием гармонических функций.
Белов Д.И., Волков В.Н.
Гродненский государственный медицинский университет.
(Материалы конференции 2003: 65-68)

Введение.

Качественная и количественная трактовка ЭКГ в недостаточной степени обеспечивает объяснение экспериментальных и клинических наблюдений, поскольку является чрезмерным упрощением электрических процессов, происходящих в сердце, из-за сложности его структуры и в отношении геометрической формы, и в отношении электрических свойств. Адекватным способом изучения электрических явлений в миокарде является эпи- или эндокардиальное картирование с последующим построением изохронных или изопотенциальных карт. На основании полученных данных исследователи формулируют математические модели электрического процесса в сердце и предлагают на их основе решение прямой электрофизиологической задачи – определение электромагнитного поля заданного генератора в заданной среде. Сложность проведения инвазивного исследования с регистрацией множественных отведений на открытом сердце резко ограничивает использование этого метода. В связи с этим возникает необходимость решения "обратной задачи" электрокардиографии – определения электрических событий в сердце на основании регистраций, осуществляемых на поверхности тела. Решение проблемы реконструкции возбуждения миокарда в двух- или трехмерном пространстве по данным поверхностной регистрации потенциалов позволит проводить точную визуальную и количественную топическую диагностику очаговых поражений миокарда.

При создании простой биофизической модели область возбуждения миокарда определяется как совокупность диполей, а окружающие ткани – как бесконечная гомогенная среда. Математическая модель описывается уравнением:


Обратная задача теории потенциалов описывается уравнением:



уравнение (1) может быть представлено системой уравнений: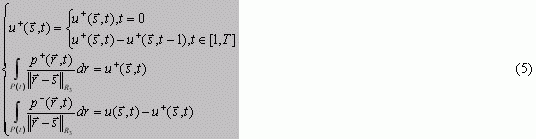
Учитывая теоремы (1 и 3) и условия (4) система уравнений (5) имеет единственное решение. С биофизической точки зрения условие (4), описывающее мультидипольную модель, в отличие от других моделей обладает следующими существенными различиями:

1. Разработанная модель с использованием метода регуляризации Тихонова (5) является стабильной.

2. Благодаря отсутствию исходных параметров позиционирования, направления и времени активации диполей, модель обладает гибкостью.

3. Основываясь на направлении распространения возбуждения в желудочках, было введено ограничение по негативным зарядам диполей в компакте P’(t) тесно связанных с позицией и абсолютным значением позитивных зарядов диполей P’(t-1).

4. Для решения (5) необходимо иметь исходное значение . Из общепризнанных экспериментальных исследований известно, что возбуждение начинается с эндокарда. Если эндокардиальная поверхность P(0) аппроксимирована поверхностью Ляпунова, то уравнение (1) имеет единственное решение, использовав которое можно вычислить .

Картирование.

Известно, что электрические явления в сердце на поверхности тела можно описать в виде полного распределения потенциалов, часто называемого “карты поверхности”. Интерпретация электрической активности сердца, основанной на полных распределениях потенциалов, имеет несколько существенных преимуществ. Во-первых, имеется уверенность в том, что не упущены никакие значимые данные, которые могли бы быть получены при измерениях на поверхности тела в других точках; во-вторых, изучение всего распределения потенциалов помогает умозрительно коррелировать картину распределения потенциалов, наблюдаемую на поверхности тела, с существующей на поверхности эпикарда.

Рассмотрим задачу нахождения решения, приближенно описывающего процесс распространения возбуждения в миокарде. Для каждого момента возбуждения имеем совокупность заряженных клеток, от которых или к которым радиально течет ток. Расположим вектора отведений вокруг некоторой точки, взятой внутри модели тела, причем все вектора должны лежать в одной плоскости. Известно, что показания на датчике, который соответствует некоторому вектору отведений, есть скалярное произведение вектора суммарного тока и вектора отведения. Таким образом, если в сторону датчика течет ток, то на датчике фиксируем положительный потенциал, в противном случае отрицательный. Проведем через концы всех векторов некоторую кривую. Очевидно, что для данного момента времени эта кривая характеризует фронт возбуждения миокарда в интегральном смысле. В качестве примера на Рисунке приведены результаты моделирования условного возбуждения на двухмерной матрице.

Рисунок. Результаты машинного моделирования возбуждения в одной плоскости. Сплошные кривые – произвольные траектории движения заряженных частиц; окружности – восстановленные по имеющимся потенциалам искомые траектории.

Дальнейшим развитием данной модели стало бы получение не одной кривой, а целой совокупности кривых, образующих некоторую поверхность, например, в виде послойной модели, описывающую распределение потенциалов на поверхности тела.

Так как полученные решения вышеизложенных задач представлялись в виде совокупности плоских кривых, то для их визуализации использовался алгоритм аппроксимации выпуклыми многогранниками с задачей удаления невидимых поверхностей для послойных моделей трехмерных объектов (Белов ДИ., Садыхов Р.Х.).

Очевидно, что визуализация полученных трехмерных моделей позволяет строить изохронные карты без привлечения алгоритмов поиска изолиний, используемых для общеизвестного плоского картирования.

Выводы.

В данной работе представлена связь между обратной задачей электрокардиографии и обратной задачей теории потенциалов. В качестве основы связи предложена новая модель распространения возбуждения в миокарде. Эта модель, основанная на классическом мультидипольном генераторе, является стабильной, гибкой и имеет единственное решение обратной задачи.

Эксперименты показали, что разработанная математическая модель двух- и трехмерной визуализации возбуждения миокарда является гладкой и устойчивой, то есть непрерывные изменения поверхностных потенциалов приводят к непрерывным изменениям моделируемой функции. В дальнейшем для получения более точных решений обратной задачи, необходимо учитывать негомогенность, динамичность и ограниченность среды.